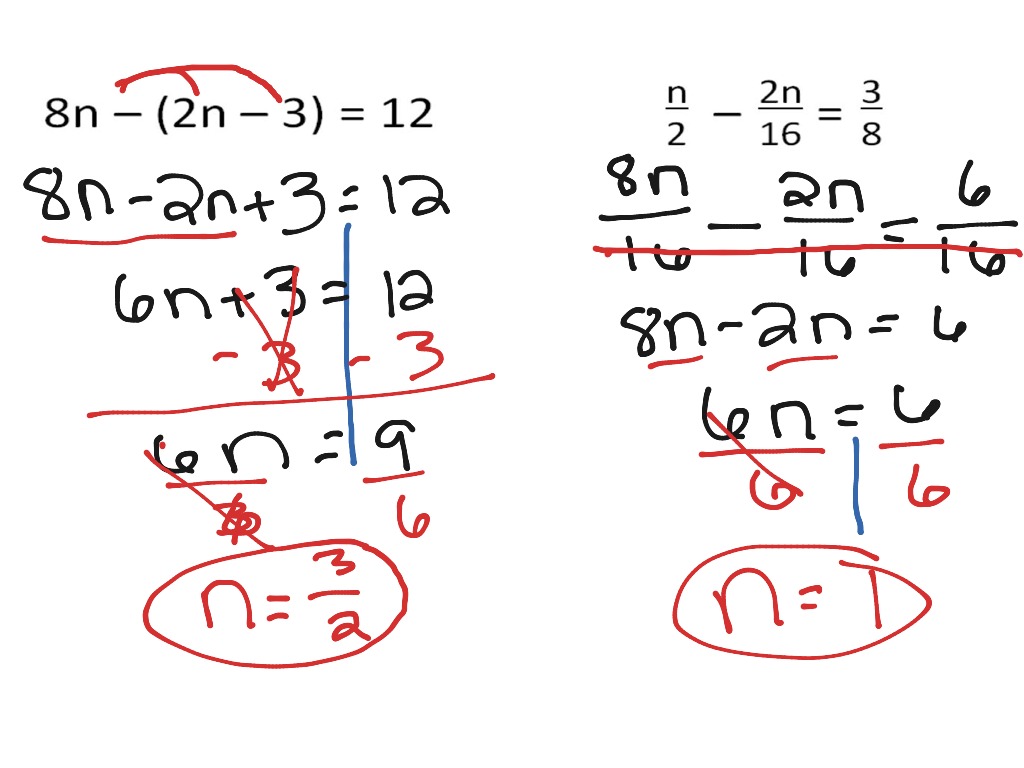
Integral calculus involves integration which is the reverse process of differentiation.įAQs on Differential Calculus What is the Definition of Differential Calculus?ĭifferential calculus is a branch of calculus involving the study of derivatives that are used to find the instantaneous rate of change of a function using the process of differentiation.These equations help to relate functions to their derivatives. There are two types of differential calculus equations - ordinary and partial differential equations.
Constant rule, difference rule, sum rule, power rule, etc., are the various rules of differential calculus.
Differential calculus involves the use of derivatives to determine the rate of change in a dependent variable with respect to an independent variable. Important Notes on Differential Calculus: Differentiation and Integration Formulas. Graphic artists use differential calculus to see how a model behaves under conditions that change rapidly. In mechanics, velocity and acceleration can be derived from the position function using differential calculus. In Biology, differential calculus is used to determine how the population of predators and prey evolves over time. In finance, differential calculus is used in portfolio optimization to choose the best stocks. Most quantitative fields use differential calculus such as complex analysis, functional analysis, abstract algebra, and differential geometry. There are wide-ranging differential calculus applications. Integral calculus is used to find areas, volumes, and central points. Integration sums up infinitesimal pieces to get the total area under a curve.ĭifferential calculus is used to determine if a function is increasing or decreasing. Intuitively, differentiation is the process of dividing something into smaller parts to track changes. Integrals are also known as antiderivatives. Integral calculus uses integrals to determine the area under a curve. In differential calculus, derivatives are used to determine the instantaneous rate of change of a function. The main points of difference between differential calculus and integral calculus are listed in the table given below: Differential Calculus Integration is the reverse process of differentiation. Let the domain be = y\)ĭifferential Calculus vs Integral Calculusĭifferential calculus uses differentiation to find the derivative of a function while integral calculus uses integration to find the integral of a function. In other words, the value of a dependent variable is determined by an independent variable.ĭomain and Range - In differential calculus, the domain can be defined as the list of all input values while the range is all the output values that are obtained after applying the inputs to a function. The value of this variable changes with respect to a change in the dependent variable. In a mathematical model, the variable that gets manipulated is the independent variable.ĭependent variable - The variable in a function that represents the output is known as the dependent variable. 
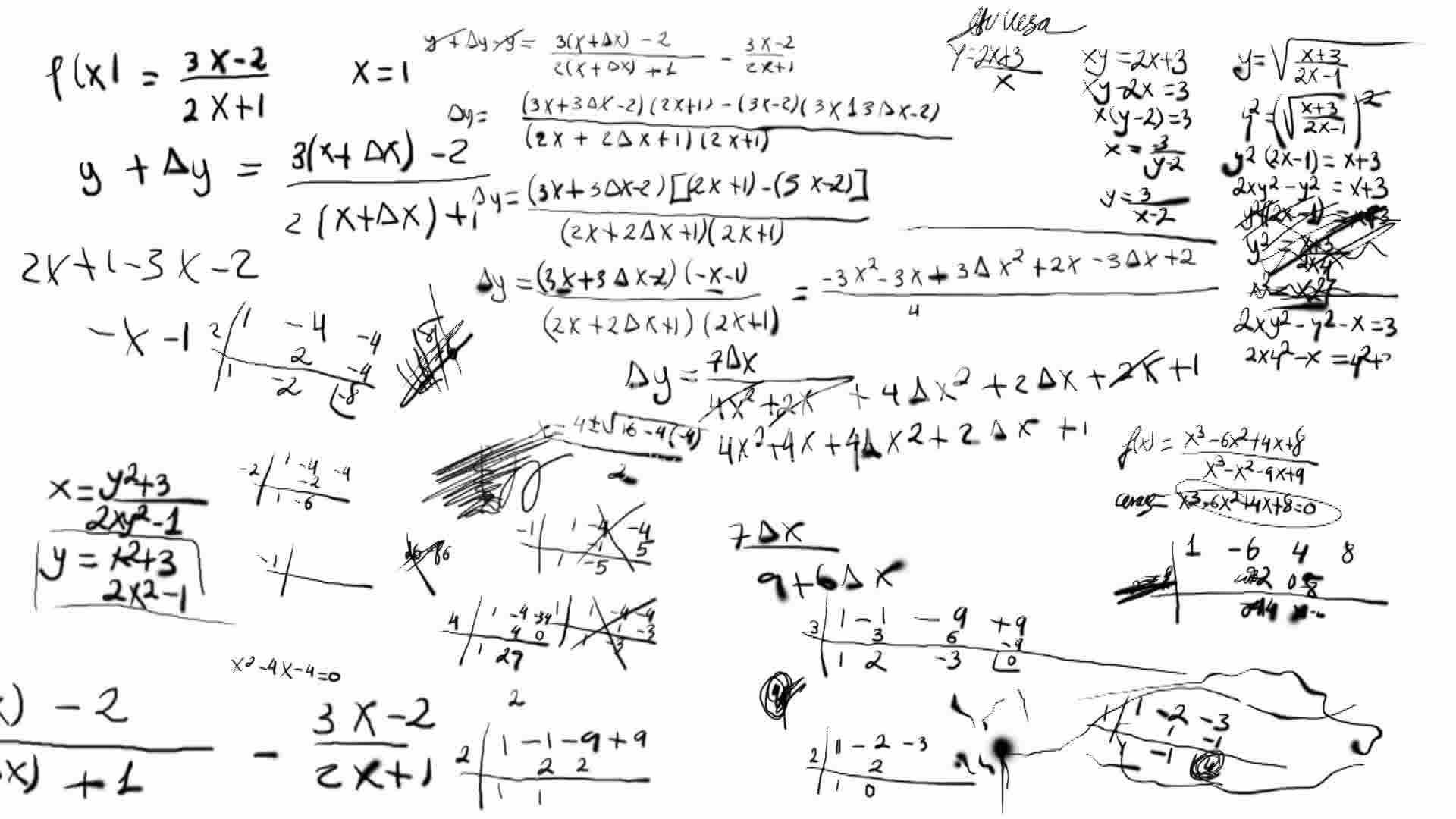
Independent variable - In a function, the variable that acts as the input is known as the independent variable. Here, x (input) is the independent variable, and y (output) is the dependent variable. Some important terms associated with differential calculus are listed below:įunction - A function is defined as a binary relation where each input is mapped to exactly one output. If y = f(x) is the function that is differentiated then, according to differential calculus, the notation is given as f'(x) = dy / dx. For example, the speed of a moving object can be interpreted as the rate of change of distance with respect to time. Differential calculus is the study of the rate of change of a dependent quantity with respect to a change in an independent quantity.
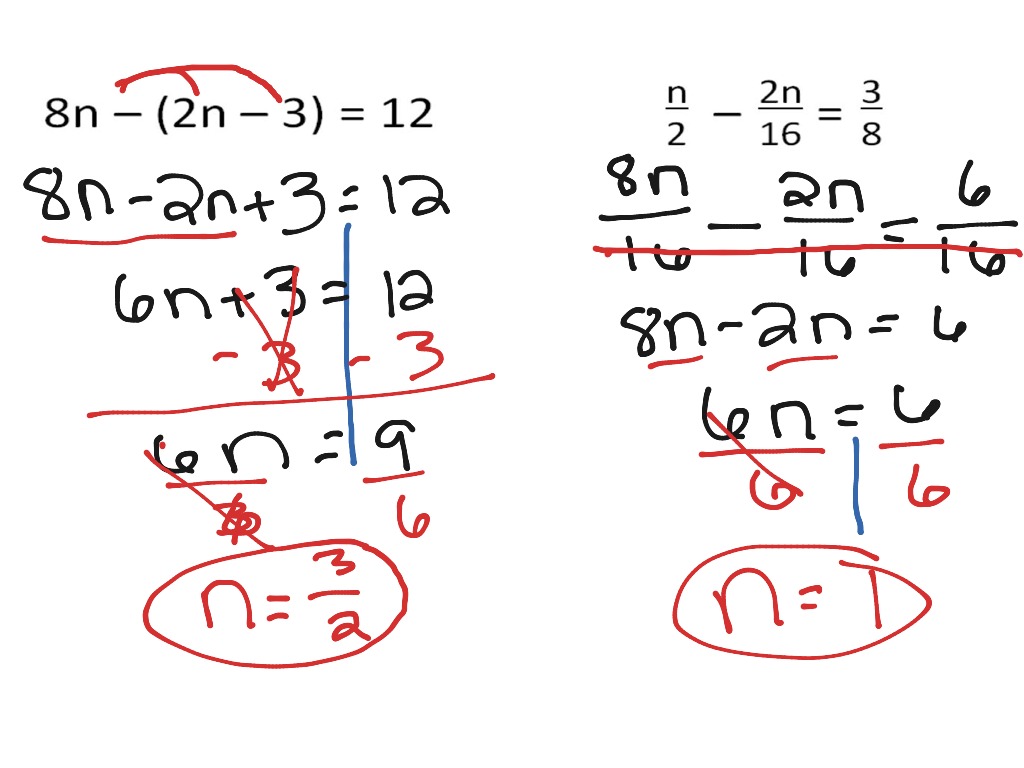
0 kommentar(er)
